- トップページ
- 基本情報技術者
- 平成18年度秋季問題
- 平成18年度秋季解答・解説
平成18年度秋季解答
問題11
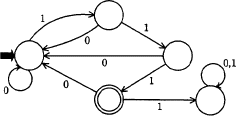
図で表される有限オートマトンで受理される文字列はどれか。ここで，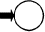
は初期状態を，
は受理状態を表す。
| ア | 01011 |
| イ | 01111 |
| ウ | 10111 |
| エ | 11110 |
解答：ウ
＜解説＞
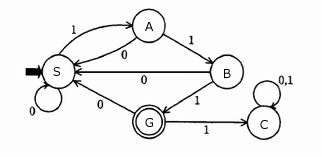
| ア | × | S | → | S | → | A | → | S | → | A | → | B |
| 0 | 1 | 0 | 1 | 1 | ||||||||
| イ | × | S | → | S | → | A | → | B | → | G | → | C |
| 0 | 1 | 1 | 1 | 1 | ||||||||
| ウ | ○ | S | → | A | → | S | → | A | → | B | → | G |
| 1 | 0 | 1 | 1 | 1 | ||||||||
| エ | × | S | → | A | → | B | → | G | → | C | → | C |
| 1 | 1 | 1 | 1 | 0 |
よってウが正解である。
問題12
四則演算の式の書き方には，演算子をオペランドの前に書く方法（前置記法），オペランドの間に書く方法（中置記法），オペランドの後に書く方法（後置記法）の3通りがある。図は，2分木で表現された式のたどり方と，各記法によって表される式を例示したものである。
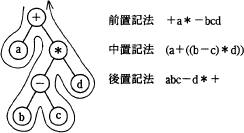
各記法で式を書く手順の説明として，適切なものはどれか。
| ア | 前置記法：節から上に戻るときにそこの記号を書く。 |
| イ | 中置記法：節に下りたときにそこの記号を書く。 |
| ウ | 後置記法：節から上に戻るときにそこの記号を書く。 |
| エ | 後置記法：葉ならばそこの記号を書いて戻る。演算子ならば下りるときに左括弧を書き，左の枝から右の枝に移るときに記号を書き，上に戻るときに右括弧を書く。 |
解答：ウ
＜解説＞
| ア | × | 後置記法：節から上に戻るときにそこの記号を書く。 |
| イ | × | 前置記法：節に下りたときにそこの記号を書く。 |
| ウ | ○ | 後置記法：節から上に戻るときにそこの記号を書く。 |
| エ | × | 中置記法：葉ならばそこの記号を書いて戻る。演算子ならば下りるときに左括弧を書き，左の枝から右の枝に移るときに記号を書き，上に戻るときに右括弧を書く。 |
問題13
表は，配列を用いた連結セルによるリストの内部表現であり，リスト［東京，品川，名古屋，新大阪］を表している。このリストを［東京，新横浜，名古屋，新大阪］に変化させる操作はどれか。ここで，A( i ， j ) は表の第 i 行第 j 列の要素を表す。例えば，A(3，1) ＝“名古屋”であり，A(3，2) ＝ 4である。また，→ は代入を表す。
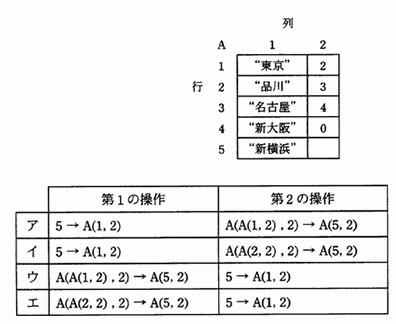
解答：ウ
＜解説＞
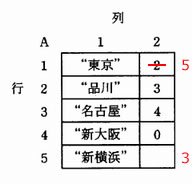
リスト［東京，品川，名古屋，新大阪］を ［東京，新横浜，名古屋，新大阪］に変化させる操作なので、 品川を新横浜に変更すればよい。
- “品川”のポインタ A(2，2)＝3 を“新横浜”のポインタ A(5，2) にセットし、行 3 の“名古屋”をポイントする。
- 次に“東京”のポインタ A(1，2) に 5 をセットし、行5の“新横浜”をポイントする。
問題14
昇順に整列されたn個のデータが配列に格納されている。探索したい値を2分探索法で探索するときの、おおよその比較回数を求める式はどれか。
| ア | log2n |
| イ | (log2n+1)/2 |
| ウ | n |
| エ | n2 |
解答：ア
＜解説＞
2分探索法は，整列済みの配列から効率よくデータを探索するための方法である。
2分探索法は、次の手順を繰り返すことによって、検索する方法である。
- 整列されたデータの中央の値と対象データを比較し、それより前方にあるか後方にあるかを判断する。
- 前方にデータがある場合は、前半分のデータの中央のデータと比較し、後方にデータがある場合は、後半分のデータの中央のデータと比較する。
要素数がn個の場合に2分探索法を使った場合の比較回数は，次の式で求めることができる。
平均比較回数：(log2 n)回
最大比較回数：(log2 n)＋1回
よってアが正解である。
問題15
次の規則に従って配列の要素A［0］、A［1］、・・・・、A［9］に正の整数Kを格納する。16、43、73、24、85を順に格納したとき、85が格納される場所はどれか。ここで、X mod YはXをYで割った剰余を返す。また、配列の要素はすべて0に初期化されている。
[規則]
(1) A［K mod 10]＝0ならば、K→A［K mod 10]とする。
(2) (1) で格納できないとき、A[ (K＋1) mod 10]＝0ならば、K→A［ (K＋1) mod 10]とする。
(3) (2) で格納できないとき、A［ (K＋4) mod 10]＝0ならば、K→A［ (K＋4) mod 10]とする。
| ア | A［3］ |
| イ | A［5］ |
| ウ | A［6］ |
| エ | A［9］ |
解答：エ
＜解説＞
16，43，73，24，85 を規則に従い、順に格納していく。
| k＝16 | A[16 mod 10]＝A[6] | 16をA[6]にセットする |
| k＝43 | A[43 mod 10]＝A[3] | 43をA[3]にセットする |
| k＝73 | Ａ[73 mod 10]＝Ａ[3] A[3]には値が入っているので、規則2より Ａ[(73+1) mod 10]＝Ａ[４] |
73 Ａ[４]にセットする |
| k＝24 | A[24 mod 10]＝A[4] A[4]には値が入っているので、規則2より A[(24＋1) mod 10]＝A[5] |
24をA[5]にセットする |
| k＝85 | A[85 mod 10]＝A[5] A[5]には値が入っているので、規則2より A[(85＋1) mod 10]＝A[6] A[6]には値が入っているので、規則3より A[(85＋4) mod 10]＝A[9] |
85をA[9]にセットする |
お問い合わせ
