平成20年度春季問題

問題6

方程式 f (x) ＝ 0 の解の近似値を求めるアルゴリズムとして知られているニュートン法に関する記述として，適切なものはどれか。

ア	y = f (x) の接線を利用して解の近似値を求めるものである。
イ	関数 f (x) が解の付近で微分不可能であっても、解の近似値を求めることができる。
ウ	異なる初期値を二つ与える必要がある。
エ	どのような初期値を与えても，必ず解の近似値が得られる。

解答・解説へ

問題7

2個の文字AとBを使って，長さ1以上7以下の文字列は何通りできるか。

ア	128
イ	254
ウ	255
エ	256

解答・解説へ

問題8

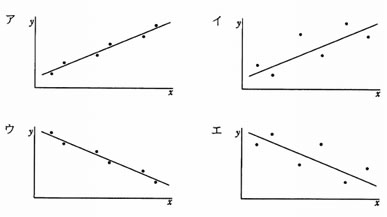
標本相関係数が－0.9，－0.7，0.7，0.9 のいずれかとなる標本の分布と回帰直線を表したグラフのうち，標本相関係数が －0.9 のものはどれか。

解答・解説へ

問題9

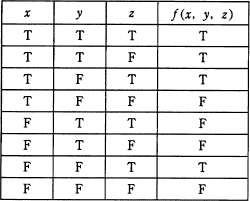
x，y，z を論理変数，T を真，F を偽とするとき，次の真理値表で示される関数 f(x，y，z) を表す論理式はどれか。ここで∧は論理積，∨は論理和， Aは A の否定を表す。

ア	(x ∧ y) ∨ (y ∧ z)
イ	(x ∧ y) ∨ (y ∧ z)
ウ	(x ∧ y) ∨ (y ∧ z)
エ	(x ∧ y) ∨ (y ∧ z)

解答・解説へ

問題10

７ビットの文字コードの先頭に１ビットの偶数パリティビットを付加するとき，文字コード 30，3F，7A にパリティビットを付加したものはどれか。ここで，文字コードは 16 進数で表している。

ア	30, 3F, 7A
イ	30, 3F, FA
ウ	B0, 3F, FA
エ	b0, BF, 7A

解答・解説へ