平成28年度春季問題
問題1
n ビットの値 L 1、L 2がある。次の操作によって得られる値L 3は、L 1とL 2に対するどの論理演算の結果と同じか。
| [操作] | |
| (1) | L 1とL 2のビットごとの論理和をとって、変数X に記憶する。 |
| (2) | L 1とL 2のビットごとの論理積をとって更に否定をとり、変数Y に記憶する。 |
| (3) | X とY のビットごとの論理積をとって、結果をL 3とする。 |
| ア | 排他的論理和 |
| イ | 排他的論理和の否定 |
| ウ | 論理積の否定 |
| エ | 論理和の否定 |
問題2
10進数123を、英字A~Zを用いた26進数で表したものはどれか。 ここで、A = 0、B = 1、…、Z = 25とする。
| ア | BCD |
| イ | DCB |
| ウ | ET |
| エ | TE |
問題3
多数のクライアントが、LANに接続された1台のプリンタを共同利用するときの印刷要求から印刷完了までの所要時間を、待ち行列理論を適用して見積もる場合について考える。 プリンタの運用方法や利用状況に関する記述のうち、M/M/1の待ち行列モデルの条件に反しないものはどれか。
| ア | 一部のクライアントは、プリンタの空き具合をみながら印刷要求する。 |
| イ | 印刷の緊急性や印刷量の多少にかかわらず、先着順に印刷する。 |
| ウ | 印刷待ちの文書データがプリンタのバッファサイズを越えるときは、一時的に受付を中断する。 |
| エ | 一つの印刷要求にかかる時間は、印刷の準備に要する一定時間と、印刷量に比例する時間の合計である。 |
問題4
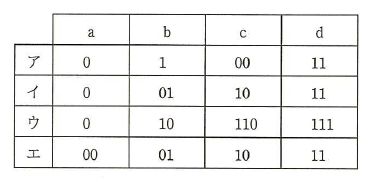
a、b、c、dの4文字からなるメッセージを符号化してビット列にする方法として表のア~エの4通りを考えた。 この表はa、b、c、dの各1文字を符号化するときのときのビット列を表している。 メッセージの中でのa、b、c、dの出現頻度は、それぞれ50%、30%、10%、10%であることが分かっている。符号化されたビット列から元のメッセージが一意に復号可能であって、ビット列の平均長が最も短くなるのはどれか。
問題5
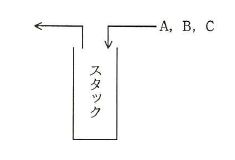
A、B、Cの順序で入力されるデータがある。 各データについてスタックへの挿入と取出しを1回ずつ行うことができる場合、データの出力順序は何通りあるか。
| ア | 3 |
| イ | 4 |
| ウ | 5 |
| エ | 6 |
お問い合わせ


