平成21年度春季解答

問題1

通信回線を使用したデータ転送システムにM/M/1の待ち行列モデルを適応すると、平均回線待ち時間、平均伝送時間、回線利用率の関係は、次の式で表すことができる。

回線利用率が0%から徐々に上がっていく場合、平均回線待ち時間が平均伝送待ち時間よりも最初に長くなるのは、回線利用率が何%を超えたときか。

ア	40
イ	50
ウ	60
エ	70

解答：イ

＜解説＞

1. 平均回転待ち時間をT_w，平均伝送時間をT_s，回転利用率をpとすると、
   

   Tw	＝	Ts×	p
   			1－p

   Tw	＝	p
   Ts		1－p

   となる。
2. 平均回線待ち時間が平均伝送時間よりも最初に長くなるのは、T_wとT_sが等しい場合なので、

   1	＝	p
   		1－p

   1－p ＝ p
   2p ＝ 1
   p ＝ 0.5
   となる。

したがって、回線利用率が(イ)50%を超えた場合、平均回線待ち時間が平均伝送待ち時間よりも最初に長くなる。

問題へ

問題2

(1+α)ⁿの計算を、1+n×αで近似計算ができる条件として、適切なものはどれか。

ア	|α|が1に比べて非常に小さい。
イ	|α|がnに比べて非常に小さい。
ウ	|α÷n|が1より大きい。
エ	|n×α|が1より大きい。

解答：ア

＜解説＞

1. nに0～3の値を代入する。
   1. n=0の場合
      (1+α)⁰=1+(α×0)⇒近似値が成立
   2. n=1の場合
      (1+α)¹=1+α⇒近似値が成立
   3. n=2の場合

      1+2α+a2	=	1+2α
      a2	=	0

   4. n=3の場合

      1+3α+3α2+α3	=	1+3α
      3α2+α3	=	0

2. n≧2で近似値が成立するためには、aⁿの項を0に近づける必要がある。
   よって、|α|を非常に小さな数にする必要がある。

したがって、(ア)|α|が1に比べて非常に小さい。が正解である。

問題へ

問題3

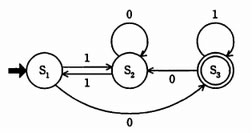
次に示す有限オートマトンが受理する入力列はどれか。ここで、S₁は初期状態を、S₃は受理状態を表している。

ア	1011
イ	1100
ウ	1101
エ	1110

解答：ウ

＜解説＞

ア	×	1011：	S1 -(1)→ S2 -(0)→ S2 -(1)→ S1 -(1)→ S2と遷移する。S2で終わるので誤りである。
イ	×	1100：	S1 -(1)→ S2 -(1)→ S1 -(0)→ S3 -(0)→ S2と遷移する。S2で終わるので誤りである。
ウ	○	1101：	S1 -(1)→ S2 -(1)→ S1 -(0)→ S3 -(1)→ S3と遷移する。S3(受理状態)で終わるので正解である。
エ	×	1110：	S1 -(1)→ S2 -(1)→ S1 -(1)→ S2 -(0)→ S2と遷移する。S2で終わるので誤りである。

問題へ

問題4

長さn の文字列C₁C₂…C_nの中に、部分文字列は全部で幾つあるかを表す式はどれか。ここで、空文字列(長さ0の文字列)とC₁C₂…C_n自身も部分文字列とみなす。例えば、長さ3の文字列C₁C₂C₃の中に、部分文字列はC₁、C₂、C₃、C₁C₂、C₂C₃、C₁C₂C₃及び空文字列の7個がある。

ア	2n-1
イ	n(n+1)/2+1
ウ	n(n-1)+1
エ	n!+1

解答：イ

＜解説＞

【考え方1】

1. n=1,n=2,n=3の場合の部分文字列の個数を考える。
   
2. ア～エの選択肢にn=1,n=2,n=3を代入して演算結果が1と一致するのは(イ)n(n+1)/2+1である。

【考え方2】

1. 長さ6の文字列c₁c₂c₃c₄c₅c₆をすべて数え上げると次のようになる。
   ※部分文字列なので、文字列中の文字を任意に取り出したり、順序を入れ替えたりする可能性はない。
   

   長さ6の部分文字列	：	c1c2c3c4c5c6	⇒1個
   長さ5の部分文字列	：	c1c2c3c4c5，c2c3c4c5c6	⇒2個
   長さ4の部分文字列	：	c1c2c3c4，c2c3c4c5，c3c4c5c6	⇒3個
   長さ3の部分文字列	：	c1c2c3，c2c3c4，c3c4c5，c4c5c6	⇒4個
   長さ2の部分文字列	：	c1c2，c2c3，c3c4，c4c5，c5c6	⇒5個
   長さ1の部分文字列	：	c1，c2，c3，c4，c5，c6	⇒6個

2. 1より、長さnの文字列の長さ1～nの各部分文字列の個数は次のようになる。
   

   長さnの部分文字列	・・・	1個
   長さn－1の部分文字列	・・・	2個
   長さn－2の部分文字列	・・・	3個
   ：
   長さ3の部分文字列	・・・	n－2個
   長さ2の部分文字列	・・・	n－1個
   長さ1 の部分文字列	・・・	n個

3. 2よりその総数は、1+2+3+・・・(n－2)+(n－1)+nとなる。
4. 等差数列の法則よりn(n+1)/2となる。
5. 空文字列(長さ0の文字列)も部分文字列とするので、(イ)n(n+1)/2+1となる。

問題へ

問題5

次の数式は、ある細菌の第n世代の個数f(x)が1世代後にどのように変化するかを表現したものである。この漸化式の解釈として、1世代後の細菌の数が、第n世代と比較してどのようになるかを説明しているものはどれか。

f(n+1)+0.2×f(n)=2×f(n)

ア	1世代後の個数は、第n世代の個数の1.8倍に増える。
イ	1世代後の個数は、第n世代の個数の2.2倍に増える。
ウ	1世代後の個数は、第n世代の個数の2倍になり、更に増殖後の20%が増える。
エ	1世代後の個数は、第n世代の個数の2倍になるが、増殖後の20%が死ぬ。

解答：ア

＜解説＞

漸化式を次のように変形する。

	f (n+1)+0．2×f(n)	=	2×f(n)
	f (n +1)	=	2×f (n )-0．2×f (n )
	f (n +1)	=	1．8×f (n )

したがって、(ア)「1世代後の個数は、第n世代の個数の1.8倍に増える。」が正解である。

問題へ