平成26年度秋季問題

問題1

A、B、C、Dを論理変数とするとき、次のカルノー図と等価な論理式はどれか。ここで、・は論理積、+は論理和、XはXの否定を表す。

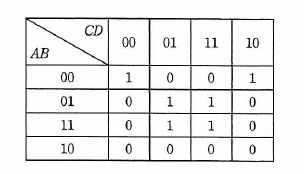s

ア	A・B・C・D + B・D
イ	A・B・C・D + B・D
ウ	A・B・D + B・D
エ	A・B・D + B・D

解答・解説へ

問題2

4n ビットを用いて整数を表現するとき、符号なし固定小数点表示法で表現できる最大値をa とし、BCD(2進化10進符号)で表現できる最大値をb とする。
n が大きくなるとa /b はどれに近づくか。

ア	(15/9)×n
イ	(15/9)n
ウ	(16/10)×n
エ	(16/10)n

解答・解説へ

問題3

コンピュータによる伝票処理システムがある。このシステムは、伝票データをためる待ち行列をもち、M/M/1の待ち行列モデルが適用できるものとする。平均待ち時間がT 秒以上となるのは、処理装置の利用率が少なくとも何%以上となったときか。ここで、伝票データをためる待ち行列の特徴は次のとおりである。

• 伝票データは、ポアソン分布にしたがって発生する。
• 伝票データのたまる数に制限はない。
• 1件の伝票データの処理時間は、平均T 秒の指数分布に従う。

ア	33
イ	50
ウ	67
エ	80

解答・解説へ

問題4

配列A[1]、A[2]、…、A[n ]でA[1]を根とし、A[i ]の左側の子をA[2i ]、右側の子をA[2i +1]とみなすことによって、2分木を表現する。このとき、配列を先頭から順に調べて行くことは、2分木の探索のどれに当たるか。

ア	行きがけ順(先行順)深さ優先探索
イ	帰りがけ順(後行順)深さ優先探索
ウ	通りがけ順(中間順)深さ優先探索
エ	幅優先探索

解答・解説へ

問題5

グラフに示される頂点V ₁からV ₄、V ₅、V ₆の各点への最短所要時間を求め、短い順に並べたものはどれか。
ここで、グラフ中の数値は各区間の所要時間を表すものとし、最短所要時間が同一の場合には添字の小さい順に並べるものとする。

ア	V 4、V 5、V 6
イ	V 4、V 6、V 5
ウ	V 5、V 4、V 6
エ	V 5、V 6、V 4

解答・解説へ