平成29年度春季問題

問題1

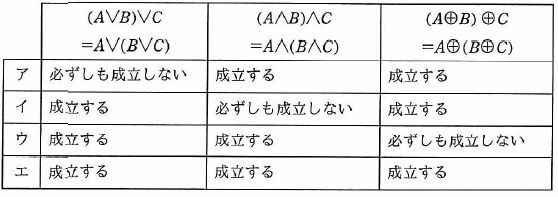
論理和(∨)，論理積(∧)，排他的論理和(⊕)の結合法則の成立に関する記述として，適切な組合せはどれか。<

解答・解説へ

問題2

(1 + α)ⁿ の計算を1 + n ×αで近似計算ができるための条件として、適切なものはどれか。

ア	| α |が1に比べ非常に小さい。
イ	| α |がn に比べ非常に大きい。
ウ	| α÷n |が1より大きい。
エ	| n ×α |が1より大きい。

解答・解説へ

問題3

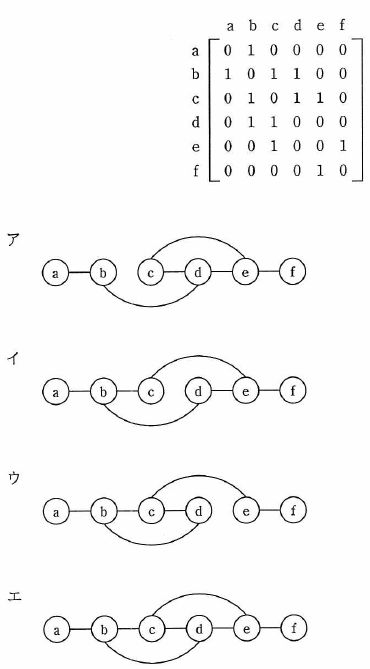
ノードとノードの間のエッジの有無を、隣接行列を用いて表す。 ある無向グラフの隣接行列が次の場合、グラフで表現したものはどれか。ここで、ノードを隣接行列の行と列に対応させて、ノード間にエッジが存在する場合は1で、エッジが存在しない場合は0で示す。

解答・解説へ

問題4

あるプログラム言語において、識別子(identifier)は、先頭が英字で始まり、それ以降に任意の英数字が続く文字列である。これをBNFで定義したとき、aに入るのはどれか。

<digit>：：= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
　<letter>：：= A | B | C | … | X | Y | Z | a | b | c | … | x | y | z
　<identifier>：：= 　　a　　

ア	<letter> | <digit> | <identifier><letter> | <identifier><digit>
イ	<letter> | <digit> | <letter><identifier> | <identifier><digit>
ウ	<letter> | <identifier><digit>
エ	<letter> | <identifier><digit> | <identifier><letter>

解答・解説へ

問題5

次の数式は、ある細菌の第n 世代の個数f (n )が1世代後にどのように変化するかを表現したものである。この漸化式の解釈として、1世代後の細菌の個数が、第n 世代と比較してどのようになるかを説明しているものはどれか。

ア	1世代後の個数は、第n 世代の個数の1．8倍に増える。
イ	1世代後の個数は、第n 世代の個数の2．2倍に増える。
ウ	1世代後の個数は、第n 世代の個数の2倍になり、更に増殖後の20%が増える。
エ	1世代後の個数は、第n 世代の個数の2倍になるが、増殖後の20%が死ぬ。

解答・解説へ